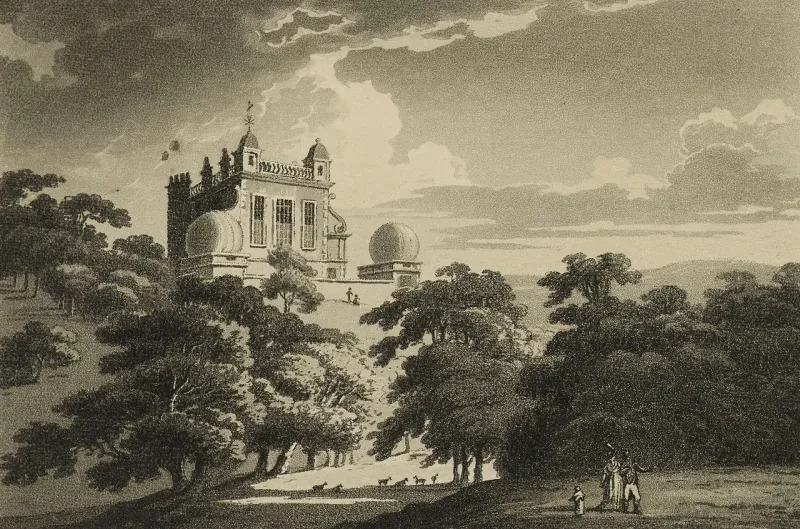How did astronomers including Nevil Maskelyne, fifth Astronomer Royal, help solve the longitude problem?
In the movies, if not in life, there are good guys and bad guys and there is one winner who takes it all. The brilliant John Harrison has long been portrayed as the plucky underdog, who challenged the notion of astronomy as a way of determining longitude. This has however tarnished the reputation of another brilliant man: Nevil Maskelyne.
Mayer, the Moon and Maskelyne
Isaac Newton’s theories within his book Principia failed to describe the Moon’s motions well enough to find longitude accurately. This flaw stimulated some of the finest mathematicians of the eighteenth century.
A brilliant astronomer in Hanover, Tobias Mayer, believed that part of the problem lay in the astronomical observations that the theories were based on. He confirmed this through a detailed analysis of historical observations and the best modern data from James Bradley, now third Astronomer Royal at Greenwich.
Sextant
Discussions of Tobias Mayer’s ideas were taking place in England by the end of 1754. James Bradley commissioned the London instrument maker John Bird (1709–1776) to make a brass copy of a repeating circle, that had been designed by Mayer.
This was refined during sea trials, and became the first marine sextant. Bradley concluded that Mayer’s tables, alongside a good instrument of this sort could determine a ship’s longitude to within 1°. This result brought Mayer’s proposal within the limits of the 1714 Longitude Act.
Nevil Maskelyne enters the story
Mayer’s ideas were trialled on a longer British voyage, an expedition to the Atlantic island of St Helena to observe the transit of Venus across the face of the Sun in 1761. Nevil Maskelyne (1732–1811), a mathematics graduate from Cambridge who was already working with Bradley, was appointed to make the transit observations and used the voyage to St Helena to test Mayer’s ideas. By the time they anchored, Maskelyne was able to report that his longitude reckoning by lunars was only 1½° in error compared to errors of up to 10° from dead reckoning.
Once he returned, Maskelyne became a huge advocate of lunars. He told the Royal Society that anyone with sufficient time and ability could now work out their longitude at sea. In actual fact, the calculations were decidedly lengthy. They would become simpler if pre-computed tables of the Moon’s future positions were produced, an idea Maskelyne got from the Connaissance des temps (the French almanac) for 1761.
Maskelyne and the Nautical Almanac
Maskelyne quickly created a system for producing the Nautical Almanac and Astronomical Ephemeris. Within months of his arrival at Greenwich in March 1765, he had established the layout and content of each almanac, providing information useful to astronomy, navigation and cartography for a year, and later several years, ahead. Work got under way, and the data for 1767 were ready to be printed by the end of 1766.
It was largely Maskelyne’s assistants who processed the observations into data ready for publication. It was tedious and poorly-paid work. The role was often seen as an opportunity for an observational and mathematical training rather than a long-term position.
The exceptional Mary Edwards
Many of the stories of individual computers make fascinating reading but Mary Edwards stands out as one of the few female contributors to this narrative. It was unusual for women at this time to have had the mathematical knowledge and training to work as computers, but Mary may have been taught by her husband and must have had a natural aptitude. She, in turn, gained enough experience to assist in teaching new computers, including her daughters.
Bringing it all together and making it work
The Board of Longitude’s work to support the lunar-distance and timekeeper methods was only a part of the story. It was also essential to show that the new techniques could be deployed in any ocean. This meant further trials, training sailors and making better charts. Marine timekeepers remained rare and expensive; it took decades to establish their reliability and for seafarers to trust them. Establishing the use of astronomical techniques, which required mathematical ability and application, was if anything more of a challenge.
One thing became apparent quite quickly. The use of traditional methods like dead reckoning would not be abandoned any time soon and those interested in the new techniques might use all methods rather than choose one.